Did you know physicists have been teleporting stuff since the 90s? First within a lab, then across the Danube, then between tropical islands, and then even to space. These experiments made news when they were published, so you may have some deja vu when I mention them. But how does it work? What stuff? Once you grasp the claim—I can make this thing disappear, and reappear somewhere else—a flood of questions beg to follow. By the end of this article, faced with such a question: we can teleport things? I hope you can answer: Yes—and here’s how…
The story of teleportation features some of the most fascinating behaviour in quantum physics. In this story teleportation means to move a quantum state (we’ll learn specifically what that is a little later) instantly across any distance, with no interluding travel. Hang on, you may ask, how can you move something instantly, if nothing can travel faster than light? Good point: Einstein’s theory of special relativity tells us that as you move quicker, your mass increases and your sense of time slows down, preventing you from going faster than light itself. Whilst special relativity makes awesome implications about our experience of time, it does set light as the speed limit of the universe and therefore (unfortunately) prohibits Star Trek-esque teleportation.

How does quantum teleportation avoid this speed limit? The catch is that you can’t teleport information, at least not instantly. When you teleport someone a quantum state, your recipient must wait for additional instructions—travelling no faster than the speed of light—to know what you’ve sent.
If you’re wondering why teleport at all in that case, the benefit is that it obviates the need for intermediate transport. We typically encode quantum states on very small and sensitive objects, like a single particle of light (a photon). This encoding is often fragile and prone to being lost to environmental noise—in technical jargon, this is called loss of coherence—which is a bit like accidentally shaking an Etch a Sketch. We need to move encoded quantum information in order to communicate, but physical travel presents many opportunities for loss of coherence. Teleportation allows you to directly transport your quantum state exactly where you want it, without that risky intermediate travel. The second set of instructions don’t need to be encoded on quantum states, so they can be sent classically after the teleport.
Ok, I’ve gone far enough without explaining what a quantum state is or how you can use one to encode information. A quantum state is just a description of the state of something—e.g. “my ceiling light is on”—but in the mathematical framework of quantum mechanics. It describes how likely that thing is to look certain ways if you were to measure it, how it will evolve in time, and how it will interact with other systems. As you can tell, a single state can be densely packed with information, but the vice versa is also true: we can densely encode information by putting a system into a specific quantum state.
To keep things simple let’s suppose you want to teleport the smallest type of quantum information: a qubit (portmanteau of ‘quantum bit’). You may have heard a qubit is like a digital bit, which is either a 1 or a 0, except a qubit can be both 1 or 0 simultaneously. This description is a bit vague, so allow me to try and provide some tangibility.
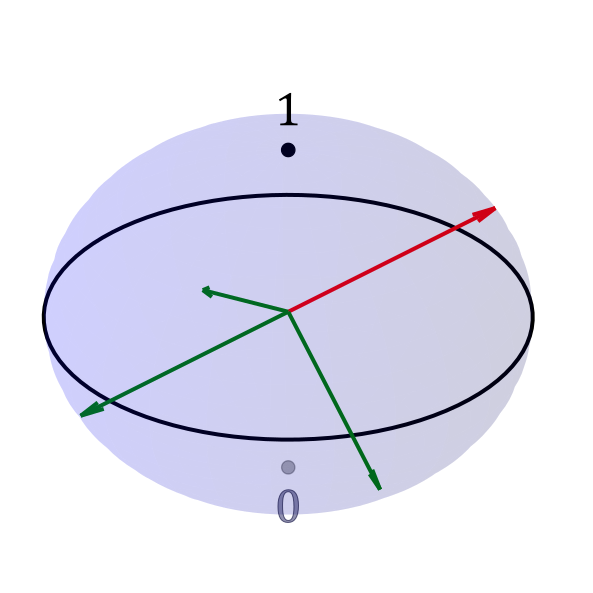
Imagine you’re Zorbing—yes, inside one of those human-sized transparent hamster balls. Or imagine you’re a very clever hamster in a normal-sized hamster ball. The parts of the ball above your head and below your feet we’ll call 1 and 0 respectively. A classical bit is either one of these two directions: if it were an arrow, it would point either straight up or straight down. Now take your hand and point in any direction you like: up down, sideways, out the entrance hole…every direction you pick is a unique value that a qubit can take. Woah.
To unpack the analogy a little more, recall that a qubit is just a quantum state and therefore describes some physical system. In particular, qubits describes systems that present in either of two possible ways when measured, and we label those presentations ‘1’ and ‘0’. The probability that the system would measure as a 1 or 0 is described by the vertical angle of your qubit arrow–for example, pointing upwards means a 1 is more likely to be measured. Additionally, the horizontal angle (azumith) of the arrow describes the phase of the system, which determines how the system will interact with other systems.
Let’s say you’ve picked a qubit arrow and you’d like to send this information to a friend. Your qubit is encoded on a photon and you’re afraid of decoherence, so teleportation seems the way to deliver it. How do you do it?
Not without help. I’m going to send two specially procured photons to you and your friend, one for each of you. Before I send them I will entangle these photons, which means they are going to be correlated—for example, they could point in opposite directions.
Entanglement is the necessary quantum physics that makes teleportation possible, so it’s worth spending a little time explaining how it works. Let’s continue the example and say the photons I’ve given point in opposite directions; now also suppose you measure which way yours points. Before your measurement, if someone asked your friend which way her photon points, she would say: “I’m not sure. Nobody knows, although we could measure it to find out.” When you make your measurement, not only do you find out which way your photon points, but because of the entanglement you also know your friend’s photon points the opposite way . If someone now asked your friend the same question again, she would reply: “I don’t know, but somebody does.” The change in information caused by your measurement creates a real, physical change in the photon’s quantum state. We say your measurement breaks the entanglement of the two photons.
Okay, back to teleportation. I’ve entangled two photons and given one each to you and your friend. You now have two photons, one from me and one carrying the qubit you want to teleport. To perform the teleport, you’re going entangle your photons by measuring them (the details of how are unnecessary here, but one way you could do this is to send them through a beam splitter). Here’s the magic: when you entangle your two photons, the maths of quantum mechanics actually force the third photon—the one I gave your friend—into a quantum state resembling your original qubit.
I say ‘resembling’ because this state could actually be one of four qubits, of which only one actually matches yours. To return to our Zorbing metaphor, these qubits will be the right sort of arrow, but they might point in the wrong direction. Fortunately, if you just tell your friend what you measured, they will know how to rotate their qubit to match the one you sent.
Something interesting about this process is that when you entangled the two particles, you destroyed your original qubit—the photon it was encoded on is wiped clean and given a new quantum state. This is why we call it quantum teleportation instead of quantum copying, and it’s a big plus for the security of the communication: the laws of physics prevent any copies being made of the qubit being given to your friend.
I should also point out that teleportation doesn’t completely remove the need for physically transporting quantum states: the entangled photons that I supply need to physically make their way to you and your friend, without losing their coherence.
That’s it! Hopefully the next time you see a quantum teleportation paper in news, you’ll be equipped to explain to your friends and family.
Thanks to Matt Whinnel for sparking this article and answering my beginner questions.